Several times a year, I get a phone call from someone wanting to know how to measure the bushels of grain in a round grain bin. There are two ways to calculate the number of bushels in a bin. The most basic method is to use the formulas we were taught in high school math class.

---

---

The Basic Method

To calculate the volume of a cylindrical object, like a round grain bin, calculate the size of the bin circle, then multiply by the height of the bin (or the grain depth if the bin is not full). This results in the cubic feet of grain in the bin. (To calculate the area in square feet of a circle multiple 3.14 (pi) by the radius squared. To square a number, you multiply the number by itself. The radius is the diameter of the bin divided by 2.)

To convert from cubic feet to bushels, multiply cubic feet by 0.8.

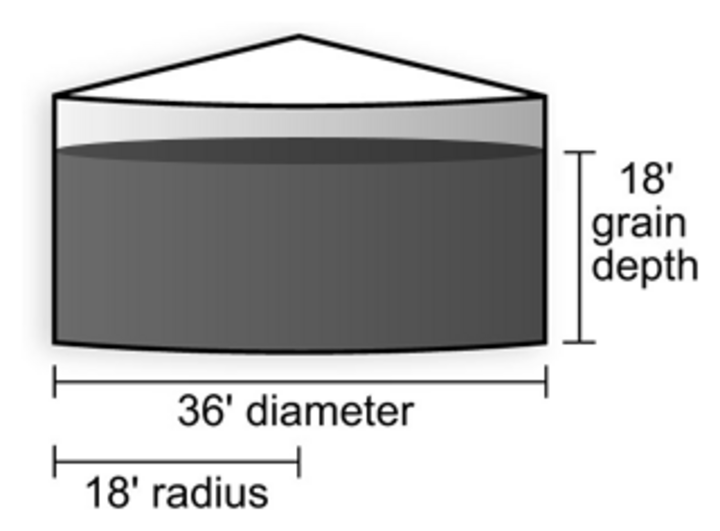
For example, with a 36-foot diameter bin, the radius would be half the diameter or 18 feet (Figure 1). To square it, multiply 18 by 18. (18 x 18 = 324). Now, multiply by pi (3.14): 324 x 3.14 = 1,017.36 square feet.

Lets assume the grain is 18 feet deep and leveled off at the top. There is 1,017.36 square feet across x 18 feet of grain depth = 18,312.5 cubic feet of grain in the bin.

The final step is to convert from cubic feet to bushels. There are 0.8 bushels in a cubic foot so multiply 18,312.5 cubic feet x 0.8 bu/cubic foot to get 14,650 bushels of grain in the bin.

The Quick Method

A second method results in the same answer in fewer steps and does not require as much algebra. The equation is:

Bu = 0.628 x D² x H

Where:

Bu is the bushels of grain the bin.
D is the diameter of the bin (ft).
H is the depth of the grain in the bin.

A conversion constant of 0.628 combines several of the mathematical operations found in the first method. Going back to the example of a 36-foot diameter grain bin holding 18 feet of grain, the bushels in the bin is calculated as follows:

Bu = 0.628 x 36² x 18 = 14,650

Tom Dorn
UNL Extension Educator